
Tietojenkäsittelyssä loogiset toiminnot ovat välttämättömiä, koska niitä voidaan käyttää mallintamaan tapaa, jolla informaatio virtaa sähköpiirien kautta, kuten CPU: n sisällä oleviin piireihin. Tämäntyyppisiä toimintoja kutsutaan Boolen-toimintoiksi.
Piirin elementtejä, jotka toimivat Boolen logiikan mukaisesti, kutsutaan loogisiksi porteiksi.
Peruslogiikkaoperaatiot
Seuraavat seitsemän logiikkaoperaatiota ottavat syötteitä, jotka ovat joko totta (1) tai vääriä (0) ja tuottavat yhden lähtöarvon, joka on myös tosi tai väärä.
Useimmat näistä toiminnoista voivat kestää enemmän kuin kaksi tuloa, lukuun ottamatta NOT-toimintoa, joka vie vain yhden tulon. Alla on esimerkkejä vain yhdestä tai kahdesta tulosta, mikä yleensä tapahtuu tietokoneen sisällä.
Toiminnot on lueteltu alla. Saat lisätietoja napsauttamalla operaation linkkiä.
- JA
- TAI
- EI
- NAND
- EI MYÖSKÄÄN
- XOR
- XNOR
JA logiikkatoiminto palaa totta vain, jos kaikki sen tulot ovat totta. Jos jokin tuloista on väärä, myös tuloste on väärä.
Tietokoneohjelmoinnissa AND-operaatio on yleensä kirjoitettu &&: ksi (kaksi osaa).
Boolen algebrassa kahden sisääntulon A ja B toiminta voidaan kirjoittaa AB: ksi .
Alla on totuustaulukko, joka sisältää kahden tulon JA toiminnon sekä JA-logiikkaportin piirikaavion.

| JA | ||
|---|---|---|
B | AB | |
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
TAI
OR-logiikkatoiminto palautuu totta, jos jokin sen tuloista on totta. Jos kaikki tulot ovat vääriä, tulos on myös väärä.
Tietokoneohjelmoinnissa OR-toiminto kirjoitetaan yleensä nimellä || (kaksi pystysuoraa palkkia).
Boolen algebrassa kahden tulon A ja B OR-arvo voidaan kirjoittaa A + B: ksi .
Huomautus: Älä älä vahingoita OR-toimintoa aritmeettista lisäystä varten, vaikka molemmat käyttävät " + " -merkkiä. Ne ovat erillisiä toimintoja.
Alla on totuustaulukko kahden tulon TAI-toiminnolle ja OR-logiikkaportin piirikaavio.

| TAI | ||
|---|---|---|
B | A + B | |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 1 |
EI
NOT-logiikkatoiminto palautuu totta, jos sen tulo on väärä, ja väärä, jos sen tulo on totta.
Tietokoneohjelmoinnissa NOT-toiminto on yleensä kirjoitettu ! (huutomerkki).
Boolen algebrassa tulon A EI-arvo voidaan kirjoittaa A̅: ksi (A ylivoimaisella).
Alla on EI-toiminnon totuustaulukko ja NOT-logiikkaportin piirikaavio.

NAND
NAND-logiikkatoiminto (joka tarkoittaa "EI JA") palautuu totta, jos jokin sen tuloista on vääriä, ja väärä, jos kaikki sen tulot ovat totta.
Boolen algebrassa voidaan kirjoittaa kahden tulon A ja B NAND-arvo

NAND on erottunut siitä, että se on yksi kahdesta "universaalisesta" logiikkaportista, koska mitä tahansa muuta logiikkaoperaatiota voidaan luoda käyttämällä vain NAND-portteja. (Toinen yleinen logiikkaportti on NOR.)
Alla on totuustaulukko kahden tulon NAND-toiminnolle ja NAND-logiikkaportin piirikaavio.

| NAND | ||
|---|---|---|
B | ___ AB | |
| 0 | 0 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
EI MYÖSKÄÄN
NOR-logiikkatoiminto (joka tarkoittaa "EI TAI") palaa totta, jos kaikki sen tulot ovat vääriä, ja vääriä, jos jokin sen tuloista on totta.
Boolen algebrassa voidaan kirjoittaa kahden tulon A ja B NOR-arvo
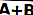
NOR: llä on ero kahdesta "universaalisesta" logiikkaportista, koska mitä tahansa muuta logiikkaoperaatiota voidaan luoda käyttämällä vain NOR-portteja. (Toinen yleinen logiikkaportti on NAND.)
Alla on totuustaulukko kahden tulon NOR-toiminnolle ja NOR-logiikkaportin piirikaavio.

| EI MYÖSKÄÄN | ||
|---|---|---|
B | _____ A + B | |
| 0 | 0 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 0 |
XOR
XOR-logiikkaoperaatio (joka tarkoittaa "Exclusive OR" -toimintoa palautuu totta, jos jokin sen tuloista eroaa, ja väärä, jos ne kaikki ovat samoja. Toisin sanoen, jos sen tulot ovat oikean ja väärän yhdistelmän, XOR: n lähtö on Jos sen tulot ovat kaikki totta tai kaikki vääriä, XOR: n lähtö on väärä.
Boolen algebrassa kahden tulon A ja B XOR-arvo voidaan kirjoittaa A⊕B: ksi . (XOR-symboli ⊕ muistuttaa ympyrän sisällä olevaa plusmerkkiä.)
Alla on kahden tulon XOR-toiminnon totuustaulukko ja sen piirikaavio:

| XOR | ||
|---|---|---|
B | A⊕B | |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
XNOR
XNOR-logiikkatoiminto (joka tarkoittaa "Exclusive NOT OR" palautuu totta, jos kaikki sen tulot ovat samat ja väärät, jos jokin niistä eroaa toisistaan. Toisin sanoen, jos sen tulot ovat oikean ja väärän yhdistelmä, tuloste on XNOR on väärä.Jos sen tulot ovat kaikki totta tai kaikki vääriä, XNOR: n lähtö on totta.
Boolen algebrassa voidaan kirjoittaa kahden tulon A ja B XNOR-arvo

Alla on kahden tulon XNOR-toiminnon totuustaulukko ja sen piirikaavio:

| XNOR | ||
|---|---|---|
B | _____ A⊕B | |
| 0 | 0 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
- Miten tietokoneohjelma luodaan?
Akku, Boolen, Idempotence, Operaattori, Ohjelmointiehdot
